Reverse Engineering for Beginners (CH1.2 Some basics)
A short introduction to the CPU
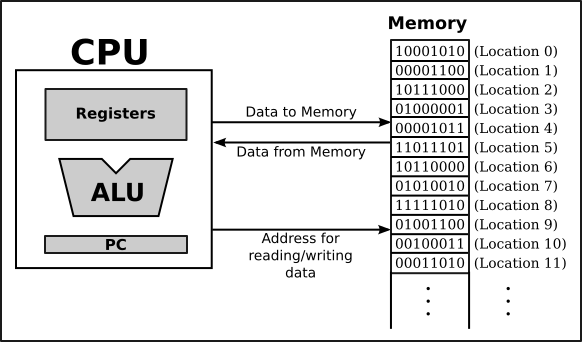
What is the CPU ?
The author began by explaining what a CPU actually is. He defined the CPU as the component responsible for executing Machine Code — the low-level instructions that programs are ultimately made of.
Then, he clarified a few important terms:
1. Instruction
An instruction is a simple command that the processor can execute — for example, moving data between registers or performing a basic arithmetic operation. Each type of processor has its own specific set of instructions that define its architecture. This set is called the ISA (Instruction Set Architecture), which will be discussed later.
2. Machine Code

Machine Code is the actual code that the CPU processes directly. Each instruction is usually encoded in several bytes.
3. Assembly Language
Assembly Language is a human-readable representation of machine code. It uses mnemonic codes and sometimes extensions such as macros. It’s designed to make programming at a low level easier for developers.
4. CPU Registers
CPU registers are very small and extremely fast storage locations used to temporarily hold data during instruction execution. Their number is limited — for example, around 8 in x86 processors, about 16 in x86-64, and roughly 16 in ARM. Because of this limitation, programmers must use them carefully.
Instruction Set Architectures (ISA)
Every CPU has its own unique instruction set architecture (ISA), which defines how it processes instructions. The author explained the two most common ones:
1. x86 Architecture (Intel & AMD)

The x86 processors (used by Intel and AMD) have variable-length instructions, meaning some instructions are short while others are longer. Because of this design, when x64 was introduced, the change wasn’t very dramatic — they simply added some new features but kept the same overall foundation.
2. ARM Architecture (Used in Mobile and Tablet Devices)

The ARM architecture is based on the RISC (Reduced Instruction Set Computer) concept — it uses a smaller, simpler set of instructions.
Originally, each instruction in ARM took exactly 4 bytes, a format known as ARM Mode. Later, developers realized that many instructions didn’t need all 4 bytes, so they created a 2-byte format called Thumb, which made the code smaller and faster.
After that, ARM introduced Thumb-2 (in ARMv7 architecture), which combined both 2-byte and 4-byte instructions and added new features. This provided the benefits of full ARM mode while keeping efficiency.
That’s why most iPhone and iPad applications use it — especially since Xcode (Apple’s compiler) does this automatically.
Finally, the ARM 64-bit (ARM64) architecture was introduced. In this version, all instructions are 4 bytes long, and the old Thumb mode was completely removed.
Numeral Systems

The author explained that nowadays, the Octal system is almost obsolete, except for one main use — file permissions in POSIX systems (like Linux).
On the other hand, the Hexadecimal system is used quite often, especially when we want to focus on the bit pattern of a value rather than its numerical meaning.
He also pointed out that humans are simply used to the decimal system because we have ten fingers — but the number “10” itself doesn’t hold any special meaning in science or mathematics; it’s just a human convenience.
In digital electronics, however, the natural way to represent information is the Binary system, because circuits are either carrying current (representing 1) or not (representing 0).
Here are some simple examples:
- 10 in binary = 2 in decimal
- 100 in binary = 4 in decimal
If a numeral system has 10 symbols (from 0 to 9), then its base (or radix) is 10. Meanwhile, the binary system has a base of 2.
The author also emphasized two important points to remember :
- The number itself is the value, but a digit is just a single symbol used to represent part of that number. For example, when you write the number 27, the digits “2” and “7” are just symbols — the full number represents the actual value, much like how letters form a complete word that has meaning.
- The value of a number doesn’t change when you convert it between numeral systems — only the representation does. For example, the number that equals “10” in decimal is the same as “1010” in binary and “A” in hexadecimal — it’s the same value, just written differently.
Converting From One Radix To Another

The author explains that almost all numeral systems use something called Positional Notation, which means every digit in a number has a specific weight or value depending on its position within the number.
For instance, if the digit 2 is on the far right, its value is 2. But if it moves one place to the left, its value becomes 20 — ten times larger simply because its position changed.
Example: 1234
1 × 10³ + 2 × 10² + 3 × 10¹ + 4 × 10⁰ = 1000 + 200 + 30 + 4 = 1234
In binary, the idea is exactly the same, except the base is 2 instead of 10.
- The first position = 1
- The next = 2
- Then 4
- Then 8, and so on...
So if we take the binary number 101011:
1×2⁵ + 0×2⁴ + 1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 32 + 0 + 8 + 0 + 2 + 1 = 43
Each bit is multiplied by 2 raised to its position number, and when you sum them up, the result in decimal is 43.
He also mentioned that ancient systems like the Roman numerals didn’t use positional notation. For example, the number 4 was written as IV, which made arithmetic operations quite difficult. That’s why positional systems became so important and widely used.
And since binary numbers are often long and repetitive, programmers came up with the Hexadecimal system, which simply groups 4 bits into one symbol.
For example, the binary number 1111 equals the hexadecimal F.
Hexadecimal Conversion Table
Now, how can we tell which numeral system a number belongs to?
- Decimal: Written normally like
1234. However, in some assemblers, the suffix d is added, like1234d. - Binary: Can appear in two ways — either prefixed with 0b (like
0b100110111) or with a trailing b (like100110111b). The book uses the 0b format in all examples. - Hexadecimal: Usually starts with 0x (like
0x1234CD) — common in C/C++. It can also end with an h (like1234CDh), which is popular in assemblers and debuggers. If the number starts with a letter (A–F), a leading zero is added (e.g.,0ABCDEFh) to avoid confusion with variables. In older machines, the $ symbol was sometimes used before the number (like$ABCD). The book uses the unified 0x notation. - Octal: This system (digits 0–7) was used heavily in older computers. Each digit represents 3 bits, which made binary–octal conversion easy. Nowadays, it’s mostly replaced by hexadecimal, except in UNIX / Linux systems — particularly in the
chmodcommand.
File Permissions in Octal (chmod)
The chmod command takes a three-digit octal number as input. Each digit represents permissions for owner, group, and others.
Each bit represents a permission: read (r), write (w), or execute (x).
For example:
Converted to binary, this is 110100100, which we can divide into three groups of 3 bits:
110 100 100
Each group defines the permissions:
- 6 → owner →
rw- - 4 → group →
r-- - 4 → others →
r--
Older systems like the PDP-8 used word sizes of 12, 24, or 36 bits — all divisible by 3, making octal convenient. Modern CPUs use 16, 32, or 64 bits (divisible by 4), which is why hexadecimal replaced it.
In C/C++, if you write a number starting with 0 (like 0377), it’s treated as octal. So 09 would throw an error since 7 is the highest valid digit in octal.
Also, when using disassemblers like IDA or JAD for Java code, you might see non-printable characters represented in octal instead of hexadecimal.
Divisibility

This concept is quite simple. If you look at the number 120, you instantly know it’s divisible by 10 because it ends with a zero. Similarly, 14300 is divisible by 100 since it ends with two zeros.
The same logic applies to hexadecimal numbers: If you see 0x1230, it’s divisible by 0x10; if it’s 0x12300, then it’s divisible by 0x100.
And in binary, it’s similar: 0b10000101000 is divisible by 0b1000.
This is useful for quickly identifying whether an address or memory block size is aligned (padded). For example, in PE files, sections usually start at addresses ending with three hexadecimal zeros:
0x41000 0x10001000
That’s because most sections are aligned to 0x1000 boundaries.
Multi-Precision Arithmetic and Radix
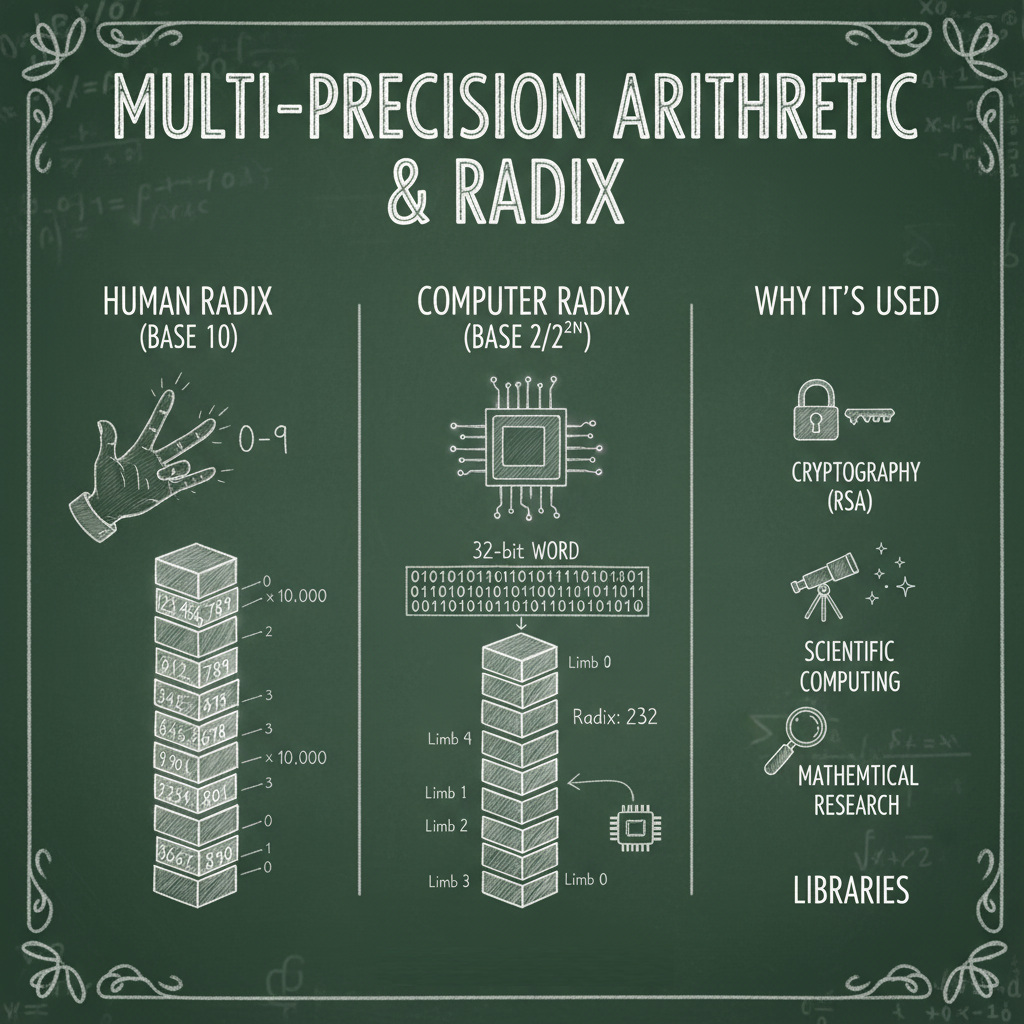
Let’s simplify this one too. When a computer performs very precise calculations with huge numbers, the processor can’t fit them into a normal integer type.
For example, RSA encryption keys can be thousands of bits long. To handle this, the large number is split into smaller parts, each treated as a separate “digit” in a base such as 2⁸ or 2³².
